A dollar today isn’t the same as a dollar tomorrow, and that’s the time value of money in a nutshell. For these reasons, we can boil down the time value of money into two fundamental principles – more is better than less, and sooner is better than later.
If you are to risk a dollar, you expect gains of more than just your dollar back. For each unit of risk you take on, you expect a slightly higher return. Even though these money concepts are easy to simplify, I want to dig deeper into each.
Editor's Note
What Is the Time Value of Money?
The time value of money means your dollar today is worth more than your dollar tomorrow because of inflation. Inflation increases prices over time and decreases your dollar’s buying power.
Time Value of Money
Money today is worth more than tomorrow’s because of inflation (on the side that’s unfortunate for you) and compound interest (the side you can make work for you).
Inflation increases prices over time, which means that each dollar you own today will buy more in the present time than it will in the future. This is why investing is so important.
Inflation is reported on an annualized basis. That means that to invest a dollar today, you’d have to expect to exceed inflation and have some wiggle room to account for the uncertainty of the future cash flow.
Over time the stock market beats out inflation. So if you put the same amount of money in a savings and investment accounts, the money invested would be worth far more than the money sitting in the savings account.
We love M1 Finance because it’s the single best and cheapest way to invest automatically in the market average – something we’re obsessed with.
Their easy-to-use platform is great for new investors. Their retirement guide will tell you exactly how much you need to save to meet your future goals. Take a look.
They're perfect for DIY investors who prefer a hands-off approach but can still pick individual stocks and funds. We specifically use them for the Golden Butterfly portion of our portfolio.
Get our best strategies, tools, and support sent straight to your inbox.
Opportunity Cost
For every choice made, there are choices sacrificed. The decision to go to college is a simple example of opportunity cost.
Choosing to attend means you are giving up four years’ worth of salary you would have earned at a job and four years of work experience (future payment.)
Of course, you hope that by choosing to go to school, you will make more money over your lifetime than if you don’t attend. So it’s a gamble, but a calculated one that hopefully will eventually have a more significant payoff than if you had chosen not to go to college.
The time value of money varies and involves an opportunity cost.
That means that if you’re putting $1,000 in a savings account to save for a house, you may be giving up an opportunity to grow that money in an investment account.
For example: Calculating the time value of your money will tell you that instead of investing, you should be paying down your 24% APR credit card debt that’s costing you hundreds a month.
Compound Interest
What’s the point of investing money if it won’t grow faster than inflation? You’d be better off spending it now when it has a higher value. That’s where the compound annual interest rate comes to the rescue.
When looking at investments like stocks, you expect the annual percentage rate to be 5% a year or 7% if you count dividends. If you have a $100 stock that increases 5% by the end of the year, you have $105 in that compounding period.
By the end of year two, it’s grown another 5% and is worth $110.25 ($105*1.05). While that’s only an extra 25 cents, in this case, over long periods and with substantial dollar amounts, that can end up being a lot of money.
It’s possible to earn interest monthly or even daily – this is called continuous compounding. This means that your balance grows by a small amount every instant.
Time Value of Money Calculator
Assuming you have a financial calculator or access to the internet, it’s pretty easy to see how much your current cash flow would be worth tomorrow, though you do have to make some assumptions.
Plenty are available online if you’re not a money nerd like me and don’t have a financial calculator sitting next to you. Here’s one from fncalculator.com. If you’ve never used one before, here’s a step-by-step breakdown of what the terms mean:
PV: This means present value. Enter how much money you have today. If you have $20 in your wallet, enter 20.
Rate: This is the rate of growth. If you’re calculating how much inflation will be, you can use a number like 3%. If you’re trying to see what your money will grow if you’re getting a 7% real (after inflation) rate of return, use 7%. You put in the whole number (7) instead of the actual decimal number (0.07).
PMT: This means payment. It’s the amount that you’re adding to the PV per period. Think of it as a monthly contribution to an IRA (assuming you’re doing monthly compounding).
Periods: The number of times you’re compounding your money. It’s essential to keep in mind how extended a period is – are you compounding weekly, monthly, or annually?
FVA: This is your future value of money. If you’re trying to calculate what your money will be worth in the future once you’ve made payments and had to compound, you’ll see your answer here.
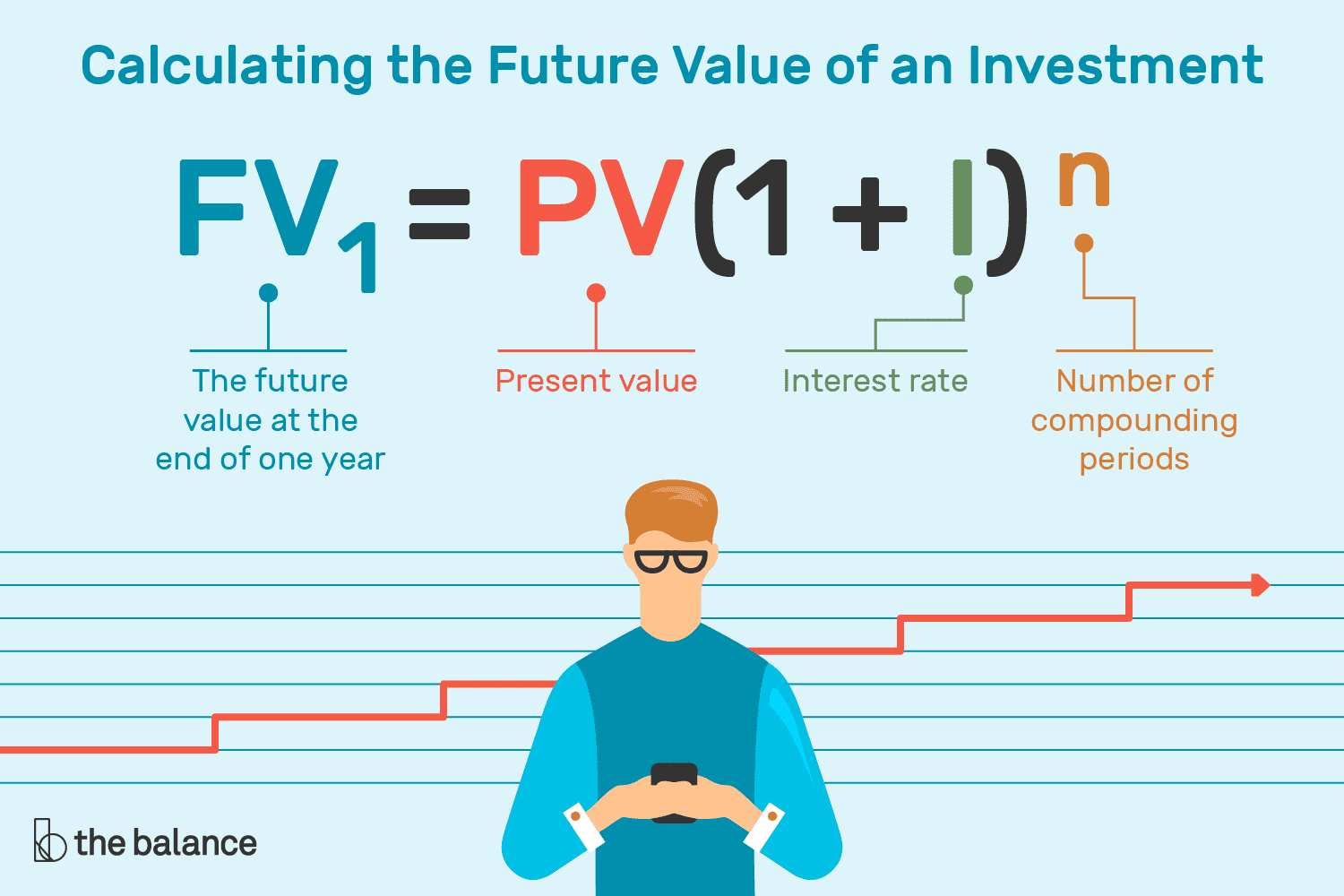
If you’re trying to reverse engineer what a future sum of money is worth today with deflation, you start with this number. And if you want to put your math hat on, the following formula is to calculate this:
Using the Time Value of Money Formula
Are you bored yet? I promise you it’s essential. With those variables, you can answer questions like these:
How much money would I need to save starting today if I wanted to have $1,000,000 in 20 years, assuming a 6% growth after inflation?
Enter 6% for rate, nothing in payment, future value $1,000,000, net present value $0, and 20 periods. Please, try it yourself! You could do this for anticipated future costs like weddings, school costs, buying a house, or anything else you want to save for.
If I start with nothing today and put away $100 a month, what will I have in 10 years if I get a 4% growth after inflation?
Here we use net present value 0, payment 1200, rate 4, ten periods, and solve for future money. Again, I recommend you try it, but I get $14,407. This question is great for seeing where you’ll be if you start today.
I occasionally go through these hypotheticals because it’s always fun to watch how my money would work for me.
When working with the calculator, one important note is that either present value, future value, or payment amounts are a negative number or 0.
A negative denotes a cost, so a negative payment is a payment into the account, and a net present negative value means you paid for it with your own money. It’s what you need to do to buy the future value.
Risk And Return
Now that you can calculate the TVM (time value of money), it’s time to look at risk and return. From example 1, we know that you would need to save a whopping $2,308 per month to get from $0 to $1,000,000 in 20 years with a 6% growth.
If you’re like me, that number seems pretty high. We need to look at securing a higher rate of return to drop that amount. A 2% higher return would lower the monthly savings by $500, but what does that mean for your investing strategy?
You’re unlikely to get extra return without taking on additional risk. Investing in a small startup is a more significant risk than investing in a well-established company, but the investment in the startup has the potential for a bigger payoff after several years.
You must be comfortable with and aware of the amount of risk in your investing strategy. If you can stomach the lows and highs that come with extra risk, it could make sense to strive for the extra return and, in turn, lower your monthly payment value.
Time Value of Money Examples
Buying a car
So, you have decided to buy a car that costs $18,000.
The car dealer gives you two choices:
1. Purchase the car for cash and receive a $2,000 instant cash rebate. This will make your out-of-pocket expense $16,000 today.
2. Or purchase the car for $18,000 with a zero percent interest 36-month loan. In this scenario, you would make monthly payments with a market interest rate of 4%.
Which is the cheaper option, and how much will you save?
The correct answer is option 1: it will save you $935.38.
A mistake people make is comparing $16,000 to $18,000. If you choose Option A, you are paying out $16,000 now. If you choose Option B, you are paying monthly installments of $500 for 36 months totaling $18,0000.
In finance, the key thing to understand is you need to compare cost always at the same point in time.
This is why it is essential to understand money’s time value.
Investing Your Money
If I offer you the choice of $1,000 right now or $1,000 five years from now, it’s a no-brainer. The $1,000 now is the answer.
But what if we change it up and offer you $1,000 right now or $1,250 five years from now? If we took the money now and invested it, would we end up with more than $1,250 or less?
Say we took the $1,000 now, invested it in the market, and made a conservative 5% interest. In one year, we’d earn $50 in interest (5% of $1,000), so our $1,000 would have grown to $1,050.
If we reinvest those gains the following year, we get a little more: $52.50 (5% of ($1,050). Each year, the interest keeps increasing or “compounding.”
By the end of year 5, we will have $1,276. So if we know we can get that 5% return, we’d be better off taking the $1,000 now rather than the $1,250 later.
Real Estate and Leverage
In the stock market, you use 100% of your money to control 100% of your investments. In real estate, you only use 20% of your money to control 100% of a property.
When you sell that property or generate monthly income on that property, you are making money on the full value of the investment. Your returns are multiplied.
To understand how leverage works and what it has to do with the time value of money, let’s look at the example of three people who have $100,000 to invest in real estate.
Person A bought a $100,000 investment property. After taxes, insurance, and property management fees, the property generated a cash flow of $500 a month.
At the end of the year, Person A will have made $6,000, a 6% return on investment. Not bad.
Person B took that same $100,000 but instead of putting it all in one property; they invested $20,000 into five different investment properties. After mortgage payments, taxes, insurance, and property management fees, the properties generated a cash flow of $200 a month per house.
At the end of the year, Person B will have made $12,000 – a 12% return on investment. That’s double the return on the same $100K initial investment.
Not only is Person B making more money than Person A, but she also controls $500,000 worth of real estate, compared to only $100,000, which means more opportunities for home value appreciation and lower risk since Person B is better diversified with five different renters.
Our proven, data-driven approach to building a portfolio of income-producing rental properties that perform in the long-term.
Why Is the Time Value of Money Important?
These concepts are the basis of every recommendation you see, even if the person making the recommendation isn’t explicitly aware of it.
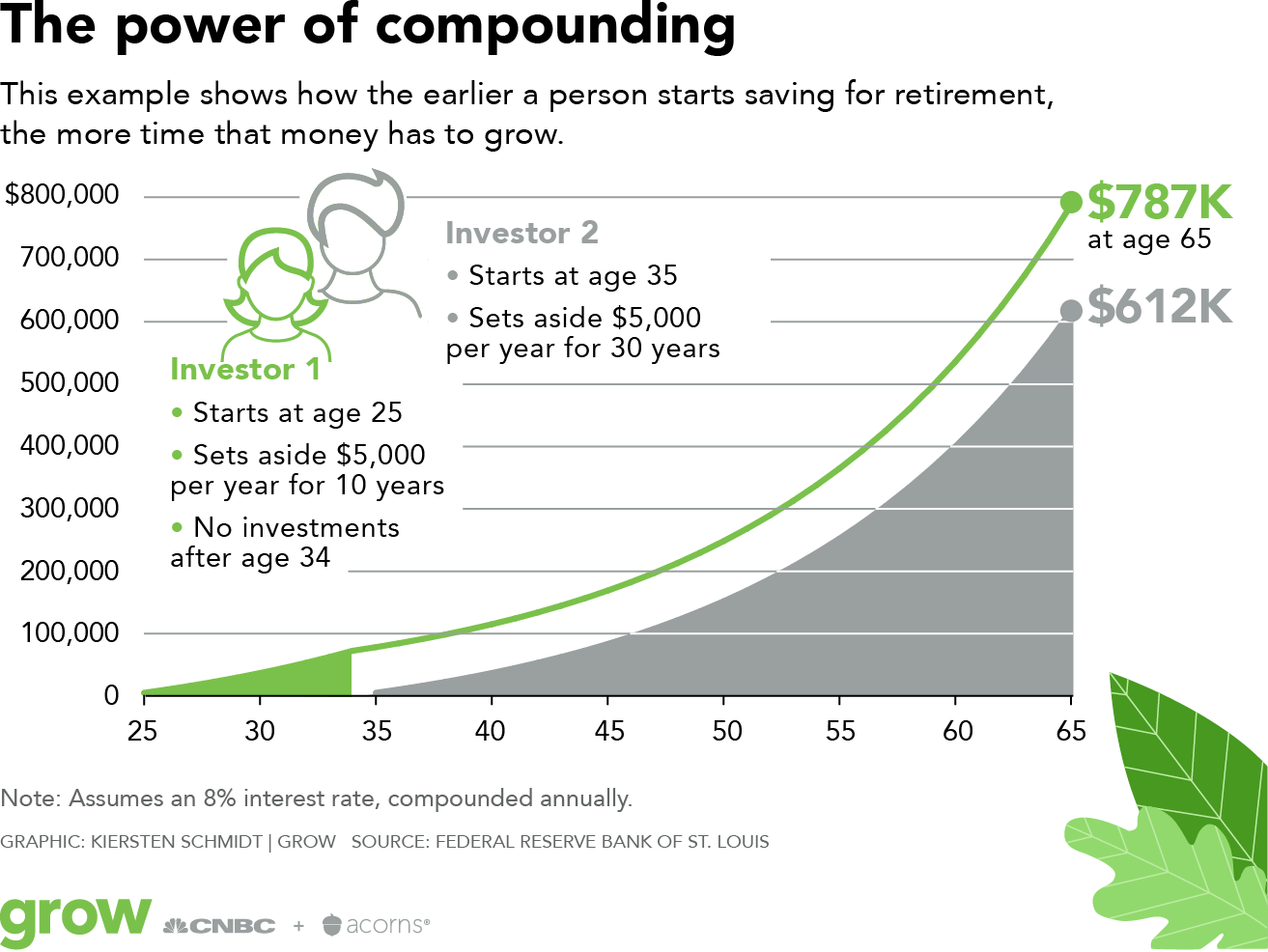
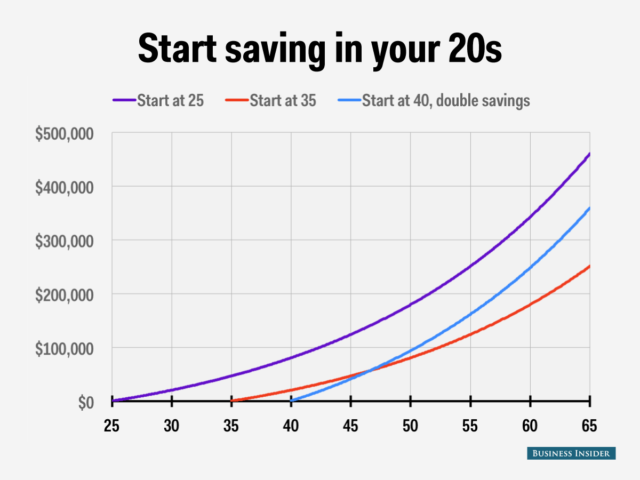
It’s better to invest early because of the TVM concept. Each dollar you invest now has a time period to grow, but it’s important to invest that dollar instead of sitting on it because if it doesn’t grow and outpace inflation, you will lose purchasing power over time.
Gas, movie tickets, and food used to cost less, and a $50,000 salary used to mean a lot more. That fantastic investment that promises a huge return? It also comes with increased risk, or it would have been snapped up already.
Again, that doesn’t necessarily mean it’s a bad financial decision; you need to understand what you’re getting into. You need to take some risk for your money to outpace inflation, so make sure you’re comfortable with the amount you’re taking.
Show Notes
Mikkeller Brewing Passion Pool – Gose-style ale with Passionfruit and Sea Salt
American Solera Movement and Color Member Blend – Foeder Ale Refermented with Chambourcin and Norton Grapes





